Randomness and Uncertainty: from random noise to predictable oscillations via differential equations

This article (PDF) by Nick Trefethen in the London Mathematical Society Newsletter demonstrates an interesting relationship between what we perceive as “randomness” and what we perceive as “certainty”.

There are many ways to generate pseudo-random numbers that look perfectly “random” but are actually the output of fully deterministic processes. Trefethen gives an example of a chaotic system based on a logistic equation.

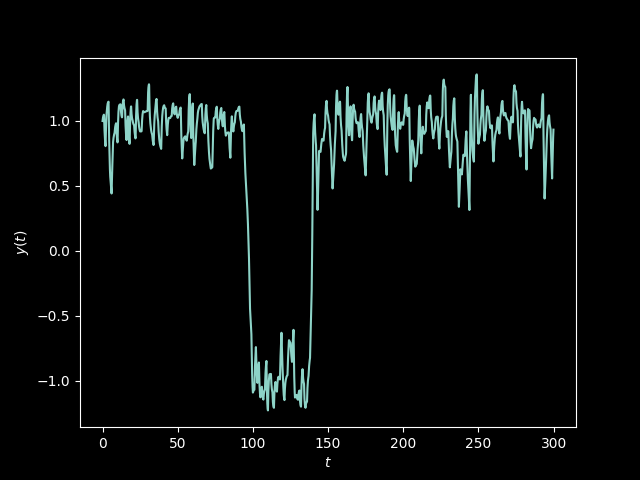
But more interesting (to me) and more original may be the other way around: how to get certainty from randomness. There are ordinary differential equations that can take random noise as input, and whose solution is very stable, oscillating between two possible values. Given a function \(f\) approximating random white noise, the solution to the ODE \[ y' = y - y^3 + Cf(t) \] is “bistable” and remains always around -1 and 1. The parameter \(C\) allows to control the half-life of the transitions.

To explore this behaviour, I replicated Trefethen’s experiments in Python with the Diffrax library (a differential equations solver based on JAX). The full code is in this Gist.

It suffices to define a simple function for the vector field and to give it to a solver:

def f(t, y, args):
    return y - y**3 + 0.4 * args[t.astype(int)]

where args will be the input, as a simple array of normally-distributed random values. \(C\) is hardcoded as 0.4 as in the article, but could be passed through args as well (it can be a dictionary).